Pricing and Adverse Selection

Author
Affiliation

Ian McCarthy, Emory University and NBER

Emory University, 2024

Overview

So far, we’ve focused on health insurance from more of an individual perspective:

  1. things health insurance does for individuals
  2. ways to improve health insurance choice or the matching between plans and individuals

But if we want people to have health insurance, and if we care about using a market to allocate health insurance, then we need to take a broader perspective

Estimating Welfare in Insurance Markets Using Variation in Prices

(see Einav, Finkelstein, and Cullen (2010) for details)

Motivation

  • Adverse selection is a central concern in health insurance markets
  • But very little empirical work in this space (until 2010 or so)

This presumably reflects not a lack of interest in this important topic, but rather the considerable challenges posed by empirical welfare analysis in markets with hidden information.

Basic Model

  • Unique feature of adverse selection: demand affects firm costs
  • Complicates welfare analysis because we need to know demand curve (how demand varies with price) but also how price changes affect costs

Setup

  • Two available contracts: high coverage (\(H\)) and low coverage (\(L\)), with relative price of \(H\) given by \(p\)
  • Consumer characteristics \(\zeta\) from distribution \(G(\zeta)\)
  • Utility denoted by \(\nu^{H}(\zeta_{i}, p)\) and \(\nu^{L}(\zeta_{i})\) for plan \(H\) and \(L\), respectively
  • \(\nu^{H}(\zeta_{i}, p)\) decreasing in \(p\), with \(\nu^{H}(\zeta_{i}, p=0)>\nu^{L}(\zeta_{i})\)
  • Costs to insurer given by \(c(\zeta_{i})\)

Demand

  • Individual \(i\) choose health insurance if \(\nu^{H}(\zeta_{i}, p)>\nu^{L}(\zeta_{i})\)
  • Denote highest price at which individual \(i\) chooses \(H\) as \(\pi(\zeta_{i}) \equiv \max \{p: \nu^{H}(\zeta_{i}, p)>\nu^{L}(\zeta_{i})\}\)
  • Aggregate demand, \(D(p) = \int 1(\pi(\zeta) \geq p) dG(\zeta) = Pr(\pi(\zeta) \geq p)\)

Supply

  • Bertrand competition with many risk-neutral insurers
  • Focus on case of perfect competition as benchmark, so that inefficiency derives from selection and not other factors
  • Costs to insurer given by \(c(\zeta_{i})\)
  • Average costs are then, \(AC(p) = \frac{1}{D(p)} \int c(\zeta) 1(\pi(\zeta) \geq p) dG(\zeta) = E(c(\zeta) | \pi(\zeta) \geq p)\)
  • Marginal costs, \(MC(p) = E(c(\zeta) | \pi(\zeta) = p)\)
  • Equilibrium, \(p^{*} = \min \{p : p=AC(p) \}\)

Welfare

Measure welfare using certainty equivalent: amount that would make consumer indifferent between obtaining outcome for sure versus obtaining outcome with uncertainty, denoted \(e^{H}(\zeta_{i})\) and \(e^{L}(\zeta_{i})\), so that WTP for health insurance is reflected by \(\e^{H}(\zeta_{i}) - e^{L}(\zeta_{i})\)

  • \(CS = \int \left[ (e^{H}(\zeta) - p)1(\pi(\zeta) \geq p) + e^{L}(\zeta) 1(\pi(\zeta) < p) \right] d G(\zeta)\)
  • \(PS = \int \left[ (p - c(\eta)) 1(\pi(\zeta) \geq p) \right] d G(\zeta)\)
  • \(TS = CS + PS = \int \left[ (e^{H}(\zeta) - c(\eta)) 1(\pi(\zeta) \geq p) + e^{L}(\zeta) 1(\pi(\zeta) < p) \right] d G(\zeta)\)
  • Socially efficient to purchase health insurance only if \(\pi(\eta_{i}) \geq c(\eta_{i})\)

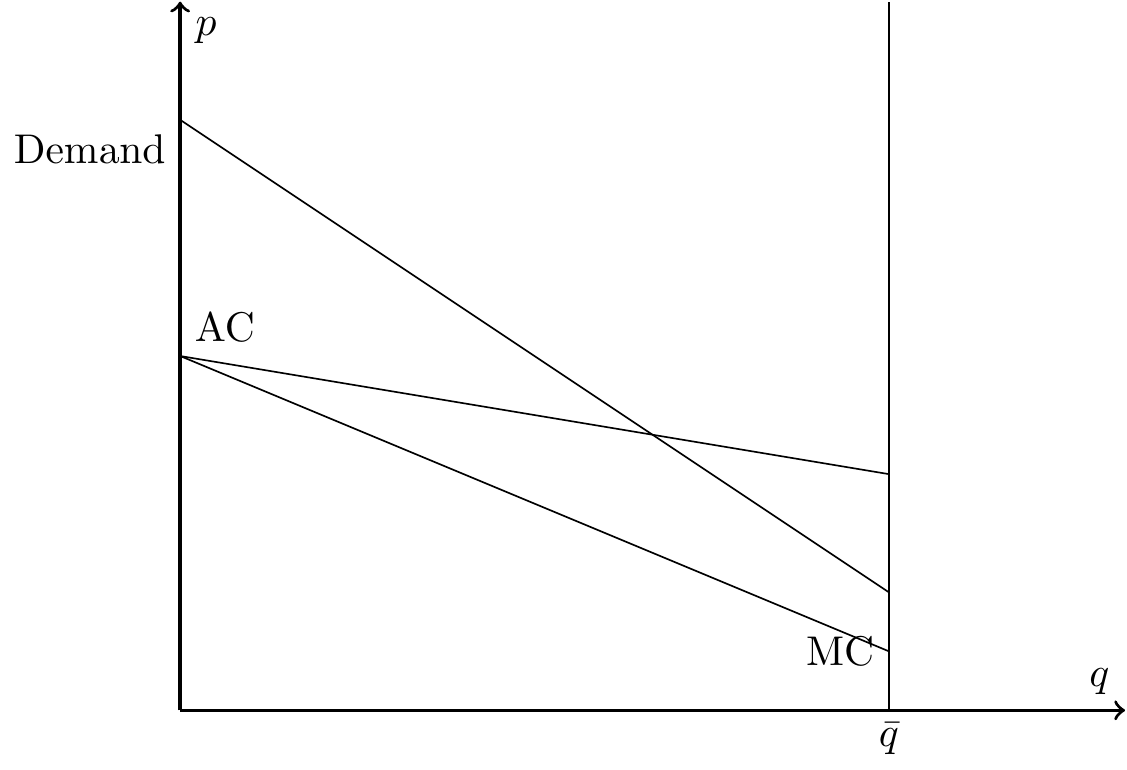
Textbook Adverse Selection

  • \(D>MC\) because willingness to pay is expected costs plus risk premium
  • Relationship between demand and AC reflects problems due to adverse selection

Main points

  • Key assumptions:
    • Simplifying assumption that insurers earn 0 profit (at least approximately)
    • Individuals select plans based on health needs (which is private information)
    • Common price to all enrollees of a given plan (community rating)
  • Possible outcomes:
    • Full insurance (Demand always above AC)
    • Partial unravelling (Demand intersects with AC somewhere)
    • Full unravelling (Demand always below AC)
  • Limitations
    • Only applies to existing contracts
    • Cannot speak to entry or exit decisions

Incorporating data

  • Goal is to estimate demand curve, \(D(p)\), and average costs, \(AC(p)\)
  • \(MC(P)\) derives from product of \(D(p)\) and \(AC(p)\)
  • Need data on:
    • prices and quantities
    • expected costs, such as claims or medical spending
    • exogenous shifters in prices

Possible sources of variation

  • State regulations introduce variation across people and over time
  • Tax policies such as health insurance subisides
  • Field experiments and “idiosyncrasies of firm pricing behavior”
  • Shifts in administrative costs of handling claims
  • Common demand instruments such as plausibly exogenous changes in market conditions

Empirical application

  • Health insurance for Alcoa employees in 2004
  • “High” versus “low” coverage PPO plans
  • Exogenous variation:
    • 7 different pricing menus for same coverage
    • Focus on relative difference, \(p= p_{H} - p_{L}\)
    • Price menus determined by president of business unit
    • 40 units in company

“As a result of this business structure, employees doing the same job in the same location may face different prices for their health insurance benefits due to their business unit affiliation.”

  • Denote medical expenditures by \(m_{i}\)
  • Denote incremental costs by \(c_{i}=c(m_{i}; H) - c(m_{i}; L)\)
  • \(c(m_{i}; H)\) is observed
  • \(c(m_{i}; L)\) computed based on terms of contract \(L\)

  • Baseline equations: \[\begin{align*} D_{i} & = \alpha + \beta p_{i} + \epsilon_{i} \\ c_{i} & = \gamma + \delta p_{i} + u_{i} \end{align*}\]

  • From those: \[MC = \frac{1}{\beta} \frac{ \partial D_{i} c_{i}}{\partial p} = \frac{1}{\beta} (\alpha \delta + \gamma \beta + 2\beta \delta p)\]

  • Find intersection points and compare to equilibrium points (\(AC(p) = D(p)\)) and efficient points (\(MC(p) = D(p)\))

Pricing and Welfare in Health Plan Choice

(see Bundorf, Levin, and Mahoney (2012) for details)

Motivation

  • Prices often not reflective of costs of coverage
  • Insurers have incentive to attract specific types of enrollees
  • Enrollees have incentive to select specific types of plans

Research question: What are the welfare effects of these forms of selection?

Setup

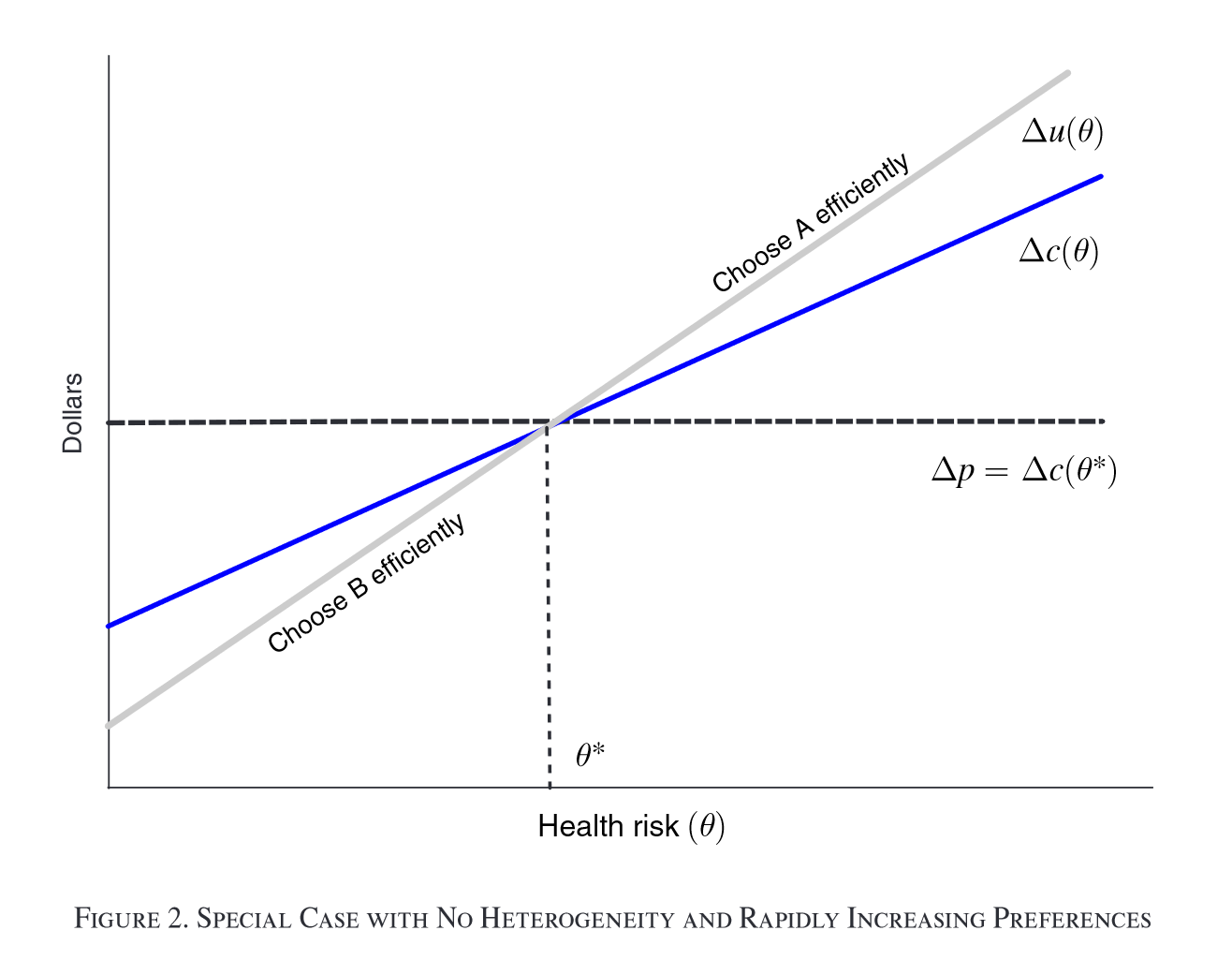
  • “Standard” setup with 2 plans
  • Assumes WTP $u $ perfectly correlated with health risk \(\theta\)
  • Assumes WTP increasing in \(\theta\) faster than costs (i.e., slope of demand curve steeper than slope of AC curve)

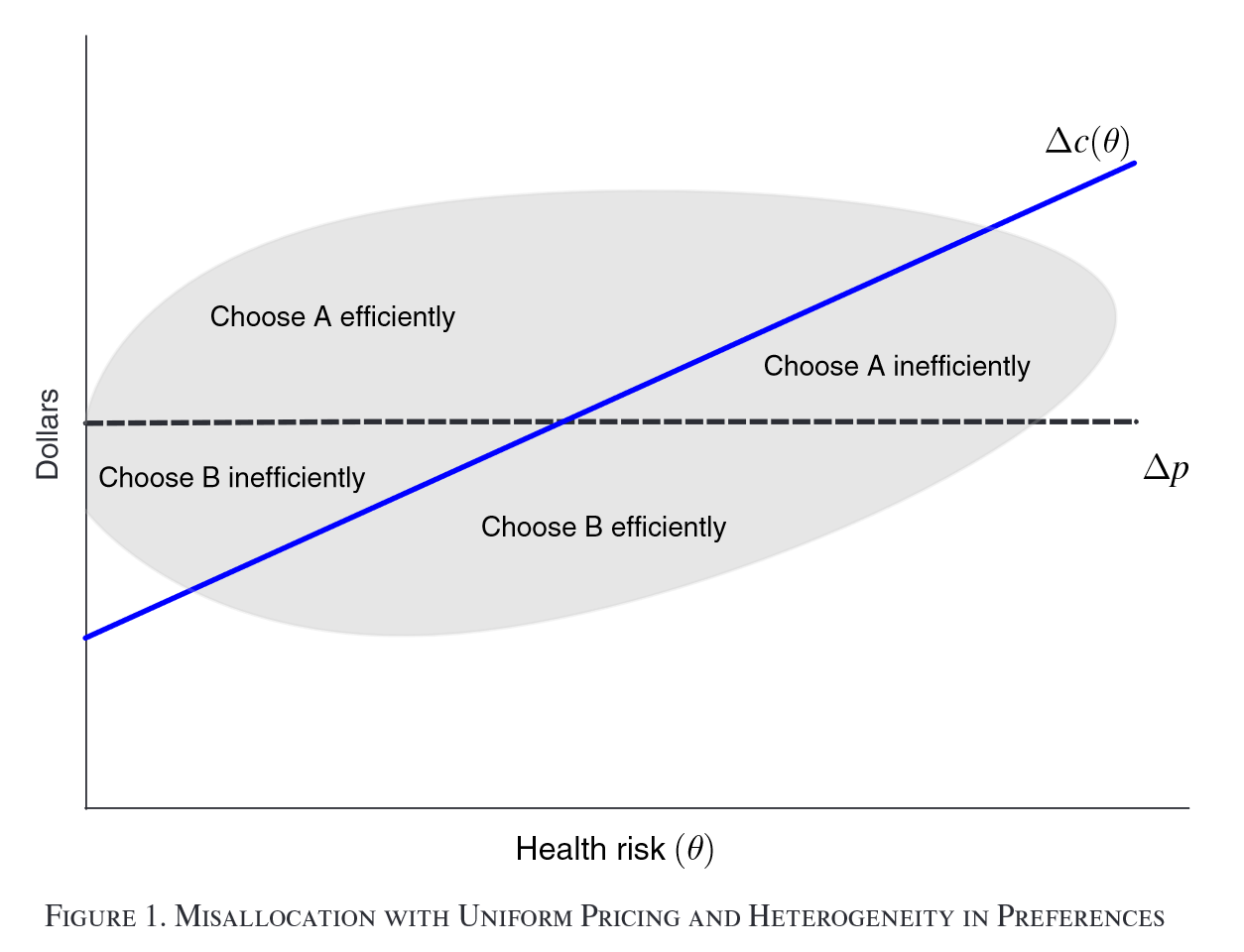
Relaxing assumptions yields potential inefficient plan allocation

Data

  • “Private firm that helps small and mid-sized employers manage health benefits”
  • 11 employers in one metropolitan area in “western United States” from 2004-2005
  • Data on 6,603 enrollees (3,683 employees), claims, plan selection, etc.

Model: Demand

Household utility: \[u_{hj} = \alpha_{1} x_{j} + \alpha_{2} x_{h} + \psi (r_{h} + \mu_{h} ; \alpha_{3}) - p_{j} + \sigma_{\varepsilon} \varepsilon_{hj}\]

  • \(x_{j}\): plan characteristics
  • \(x_{h}\): household characteristics
  • \(r_{h}\): health risk score (based on observable demographics)
  • \(\mu_{h}\): unobserved health status
  • Household \(h\) selects plan \(j\), \(q_{hj} =1\), if \(u_{hj} \geq u_{hk} \forall k \in J_{h}\)
  • Standard logit model for plan choice: \[Pr(q_{hj}=1 | x_{h}, \mu_{j}) = \frac{ \exp(v_{hj}) }{ \sum_{k} \exp(v_{hk}) },\]

for \(v_{hj} = u_{hj} - \sigma_{\varepsilon} \varepsilon_{hj}\)

Model: Costs

Costs assumed: \[c_{ij} = a_{j} + b_{j}(r_{i} + \mu_{i} -1) + \eta_{ij}\]

  • \(a_{j}\): baseline cost for standard enrollee
  • \(b_{j}\): marginal cost of insuring a higher/lower risk enrollee
  • Costs for firm-year \(f\) and insurer \(k\) are sum of all relevant \(c_{ij}\)

Model: Other things

  • Plan bids: markup over expected costs
  • Employer contribution: employers pass on share of lowest-cost plan plus fraction of incremental cost for high-cost plans

Identification and estimation

  • Need variation in prices separate from unobserved household tastes or private health risks \(\mu\)
  • Instrument for actual plan contribution using predicted contribution
  • Estimate using method of simulated moments (simulation comes from draws of \(\mu\) from normal distribution with mean 0 and variance \(\sigma^{2}\):
    • Consumer choice: \(E[q_{hj} - Pr(q_{hj}=1 | x_{h}, \mu_{j})|z_{h}, \mu_{h}] = 0\), with instruments \(z_{h}\)
    • Plan costs: \(E[C_{kf} - \hat{C}_{kf}|x_{kf}, \mu_{kf}] = 0\)
    • Plan bids: \(E[B_{if} - \hat{B}_{if}|x_{f}] = 0\)

Results

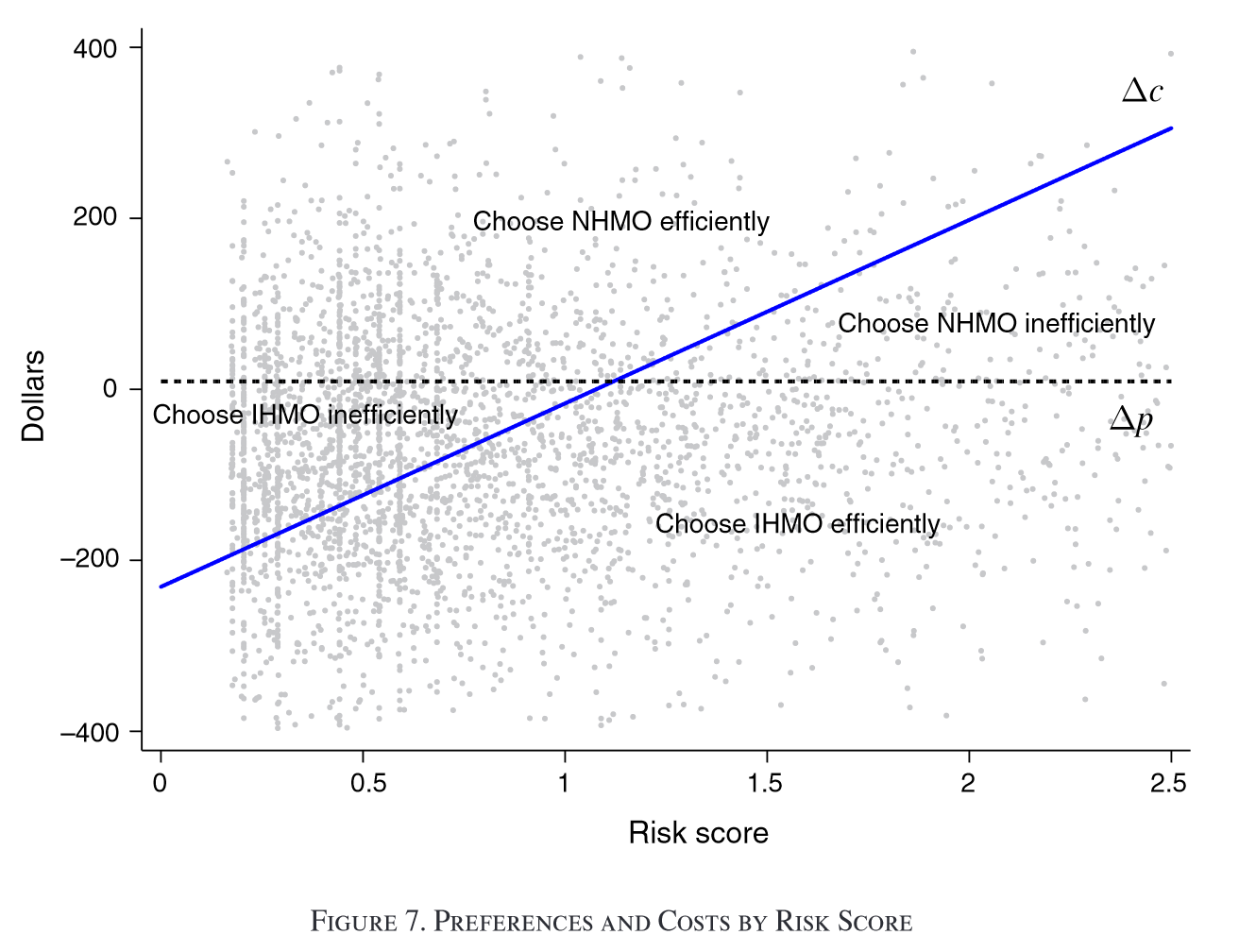
Takeaways

  • Welfare loss of 2-11% of total cost of coverage under current pricing and contributions
  • Uniform contribution policy (or community rating) offers modest improvements (1-3%)
  • Risk-adjusted premium policy can capture entirety of welfare gains

References

Bundorf, M Kate, Jonathan Levin, and Neale Mahoney. 2012. “Pricing and Welfare in Health Plan Choice.” American Economic Review 102 (7): 3214–48.
Einav, Liran, Amy Finkelstein, and Mark R. Cullen. 2010. “Estimating Welfare in Insurance Markets Using Variation in Prices.” The Quarterly Journal of Economics 125 (3): 877–921. https://doi.org/10.1162/qjec.2010.125.3.877.